Exercise 7.5 Generalize sum to a higher-order procedure that can accumulate together the elements of a list in an arbitrary fashion by using a combining procedure (such as +) specified by a procedural parameter. When the list is empty, sum returned 0, but this result isn’t appropriate for other combining procedures. For example, if the com- bining procedure is *, 1 would be the appropriate value for an empty list. (Why?) Following are two possible approaches to this problem:
a. Write the higher-order procedure so that it only works for nonempty lists. That way, the base case can be for one-element lists, in which case the one element can be returned.
b. Write the higher-order procedure so that it takes an additional argument, beyond the list and the combining procedure, that specifies the value to return for an empty list.
Solution:
a.
(define accumulate-lst
(lambda (lst f)
(if (= (length lst) 1)
(f (car lst))
(f (car lst) (accumulate-lst (cdr lst) f)))))
; b.
(define accumulate-lst-base
(lambda (lst f b)
(if (null? lst)
b
(f (car lst) (accumulate-lst-base (cdr lst) f b)))))
Exercise 7.6 a. Write a procedure that will count the number of times a particular element occurs in a given list.
b. Generalize this procedure to one that will count the number of elements in a given list that satisfy a given predicate.
Solution:
(define count-elements
(lambda (lst pred)
(if (null? lst)
0
(if (pred (car lst))
(+ 1 (count-elements (cdr lst) pred))
(+ 0 (count-elements (cdr lst) pred))))))
Exercise 7.13: The procedure map is extraordinarily handy for creating lists of all sorts. Each of the following problems can be solved by using map.
a. Write a procedure that, when given a positive integer n, returns a list of the first n perfect squares.
b. Write a procedure that, when given a positive integer n, returns a list of the first n even integers.
c. Write a procedure called sevens that, when given a positive integer n, returns a list of n sevens. For example:
(sevens 5)
d. Write a procedure that, when given a list of positive integers, returns a list of lists of integers. Each of these lists should be the positive integers from 1 to whatever was in the original list. For example,
(list-of-lists ’(1 5 3))
((1) (1 2 3 4 5) (1 2 3))
Solution:
a.
(define first-n-perfect-squares
(lambda (n)
(map (lambda (x) (* x x)) (integers-from-to 1 n))))
b.
(define first-n-even-integers
(lambda (n)
(map (lambda (x) (* x 2)) (integers-from-to 1 n))))
c.
(define sevens
(lambda (n)
(map (lambda (x) 7) (integers-from-to 1 n))))
d.
(define list-of-lists
(lambda (lst)
(map (lambda (n) (integers-from-to 1 n)) lst)))
Ex 7.14
(define my-map
(lambda (f lst)
(if (null? lst)
'()
(cons (f (car lst)) (my-map f (cdr lst))))))
Exercise 7.42: Write a procedure called apply-all that, when given a list of functions and a number, will produce the list of the values of the functions when applied to the number.
Solution:
(define apply-all
(lambda (funs x)
(if (null? funs)
'()
(cons ((car funs) x) (apply-all (cdr funs) x)))))
Exercise 7.44: Consider the following two procedures. The procedure last selects the last element from a list, which must be nonempty. It uses length to find the length of the list.
(define last
(lambda (lst)
(if (= (length lst) 1)
(car lst)
(last (cdr lst)))))</code>
(define length
(lambda (lst)
(if (null? lst)
0
(+ 1 (length (cdr lst))))))
a. How many cdrs does (length lst) do when lst has n elements?
b. How many calls to length does (last lst) make when lst has n elements?
c. Express in  notation the total number of cdrs done by (last lst), including cdrs done by length, again assuming that lst has n elements.
notation the total number of cdrs done by (last lst), including cdrs done by length, again assuming that lst has n elements.
d. Give an exact formula for the total number of cdrs done by (last lst), including cdrs done by length, again assuming that lst has n elements.
Solution:
a. n, which can be easily seen. An empty list needs 0 cdrs, a list with length 1 needs one cdrs. If we use induction, we can assume that this holds. For a list of length (n+1), we can see that length uses one cdr and then generates (length ). Therefore there are n uses of cdr for a list of length n.
b. Let’s start with the base case. (last ‘(1)) here last calls length one time. We can see that each time last have to call length. Therefore we can see that it needs n calls for a list of length n. The idea of the proof follows the last one.
c. and d. How many cdrs does last need without considering length? If the length is 1, it needs 0. If the length is 2, it needs 1. In general it needs (n-1) times cdr. We already know how often last calls length, so we can calculate the number of all calls. There are (n-1) calls from last directly. For each iteration in last we need 1 call of length. And each call of length needs (k+1) cdrs. If we merge everything together, we get the following table
len of list cdr from last calls of length cdr from length
1 0 1 1
2 1 2 2 + 1
3 2 3 3 + 2 + 1
...
n (n-1) n n + (n-1) + (n-2) + ... + 1
Now we just have to add cdr from last and cdr from length and get:

Which is 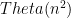 in
in  notation.
notation.
Exercise 7.47: Write a procedure map-2 that takes a procedure and two lists as arguments and returns the list obtained by mapping the procedure over the two lists, drawing the two arguments from the two lists. Write this procedure map-2. You may assume that the lists have the same length.
Solution:
(define map-2
(lambda (f lst1 lst2)
(if (null? lst1)
'()
(cons (f (car lst1) (car lst2)) (map-2 f (cdr lst1) (cdr lst2))))))