6-3. Assume that all edges in the graph have distinct edge weights (i.e. , no pair of edges have the same weight). Is the path between a pair of vertices in a minimum spanning tree necessarily a shortest path between the two vertices in the full graph? Give a proof or a counterexample.
Solution Let’s start with an example.
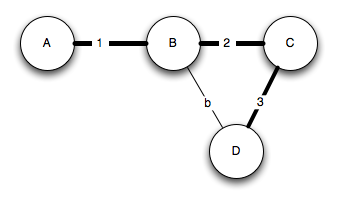
Our minimum spanning tree is marked by the thick edges. We are interested in the path between B and D. We’re interested in the weight b. If b is smaller than 5, the MST (minimum spanning tree) isn’t the shortest path. Would this change our MST? It depends. We could form the graph from B -> D -> C instead of B -> C -> D. It would be our MST if 
![e \in [0, 2] \setminus \{1, 2\}.](http://s0.wp.com/latex.php?latex=e+%5Cin+%5B0%2C+2%5D+%5Csetminus+%5C%7B1%2C+2%5C%7D.&bg=ffffff&fg=000&s=0&c=20201002)
6-6. Suppose we are given the minimum spanning tree T of a given graph G (with n vertices and m edges) and a new edge e = (u, v) of weight w that we will add to G. Give an efficient algorithm to find the minimum spanning tree of the graph G + e. Your algorithm should run in O(n) time to receive full credit.
Solution
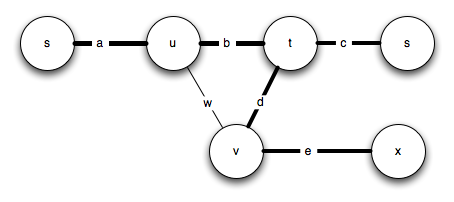
We are interested into each path going from u to v. In this example there is the initial path u->t->v and the new one u->v. Now we can check which one is shorter and take this one. The rest of the tree isn’t affected by this.
6-7. (a) Let T be a minimum spanning tree of a weighted graph G. Construct a new graph G′ by adding a weight of k to every edge of G. Do the edges of T form a minimum spanning tree of G′? Prove the statement or give a counterexample.
(b) Let P = {s, . . . , t} describe a shortest weighted path between vertices s and t of a weighted graph G. Construct a new graph G′ by adding a weight of k to every edge of G. Does P describe a shortest path from s to t in G′? Prove the statement or give a counterexample.
Solution (a) The order of the weights aren’t affected by the addition therefore it still forms the MST: 
(b) No, see the counter example in the comments by Matus Goljer. Thanks for that!
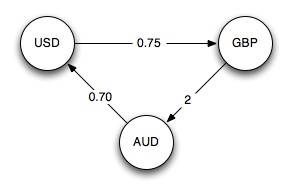
6-23. Arbitrage is the use of discrepancies in currency-exchange rates to make a profit. For example, there may be a small window of time during which 1 U.S. dollar buys 0.75 British pounds, 1 British pound buys 2 Australian dollars, and 1 Australian dollar buys 0.70 U.S. dollars. At such a time, a smart trader can trade one U.S. dollar and end up with 0.75 × 2 × 0.7 = 1.05 U.S. dollars—a profit of 5%. Suppose that there are n currencies c1 , …, cn and an n × n table R of exchange rates, such that one unit of currency ci buys R[i,j] units of currency cj. Devise and analyze an algorithm to determine the maximum value of
R[c1, ci1] · R[ci1, ci2] · · · R[cik−1, cik] · R[cik, c1]
Solution Here’s the example as a graph.
The first problem is that maximum path algorithms don’t multiply the values the add them. This problem can be solved by using logarithms:
EDIT: Please see the entry in the comments. Thanks
Can you work out the solution for the following Chapter 6 related problems:
Is the path between a pair of vertices in a minimum spanning tree necessarily a shortest path between the two vertices in the full graph? Give a proof or a counterexample.
When a vertex and its incident edges are removed from a tree, a collection of subtrees remains, as in the example below:
Prove that there exists a vertex v whose removal leaves no subtree with more than n/2 vertices.
Give a linear-time algorithm that, for any tree with n vertices, finds a vertex whose removal leaves no subtree with more than n/2 vertices. (*)
problem
Hey, at least I can try:
Generally, no. For example take this graph and its minimum spanning tree:
The shortest path in the full graph from A to C is 9 but the shortest path on the MST is 10.
You are basically looking for bridges. There’s also an algorithm on the page which works faster in this case because the tree is already a spanning tree. Hope that helps.
Thanks for these solutions; they’re great. You might want to put them on the solution wiki (http://www2.algorithm.cs.sunysb.edu:8080/mediawiki/index.php/The_Algorithms_Design_Manual_%28Second_Edition%29) because they’re severely lacking solutions for chapter 5 onwards.
Thanks! Good idea, I may have to double check some solution but if I find the time, I going to.
Hi,
Thanks for the solutions.
Regarding exercise 6.23, I think that we need to find a cycle instead of a path (i.e. at the end, we need to convert back to the original currency achieving max profit).
Also, could you please explain to me why applying the function 1/(1+e^w) to every weight does not change the shortest path?
Thanks
Hi!
Thanks for your comment. I think you’re correct.
Then it’s sadly NP-hard because we don’t have a directed acylic graph anymore: http://en.wikipedia.org/wiki/Longest_path_problem
I’m really glad for your comment because I know that a lot of people read this stuff and I don’t really have time anymore to recheck all the answers.
Thank you
You can take the -log value of each R[i,j], then look for negative cycles (which after Floyd-warshall initialized with R[i,i] = infinity finishes you can read off from the diagonal). To reconstruct the conversion rate, just reverse the -log operation.
The answer to the problem 6-7(b) is incorrect, here’s a simple counter-example
A ——- 6 ——-> B
\-1->C-1->D-1–/
Now add k = 20 to each edge. The original shortest path (A->C->D->B) now has weight 63, while the optimal path is 26 (A->B).
The issue here is that the constant k accumulates in the calcululation (for a path of length n, you are adding n TIMES k to its new overall weight).
It works when constructing the spanning tree because there the path weights don’t matter
Awesome, thanks for the correction!