Exercise 12.4: Draw a tree, analogous to Figure 4.4 on page 92, showing how the value of C(4, 2) is computed by choose. Your tree should have C(4, 2) at the root and six 1s as its leaves.
Solution: 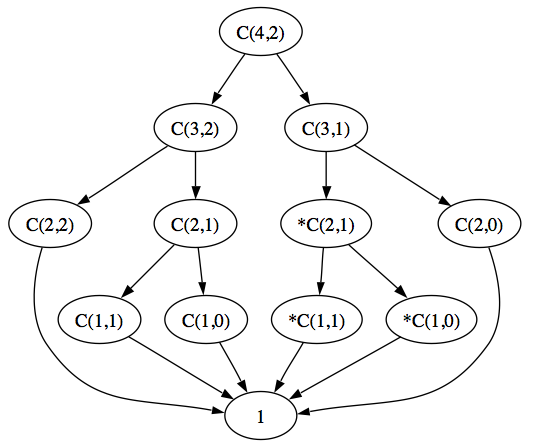
Exercise 12.6: Using these procedures, write
a. A procedure called table-fill! that takes a table and an element and sets every entry in the table to the given element. For example, (table-fill! table 0) would have a similar effect to that of zero-out-vector! in Section 11.6.
b. A procedure called display-table that nicely displays its table parameter.
Solution:
(define table-fill!
(lambda (table value)
(define loop-row
(lambda (row column)
(if (= column (table-width table))
'done
(begin
(table-set! table row column value)
(loop-row row (+ column 1))))))
(define loop
(lambda (row)
(if (= row (table-height table))
'done
(begin
(loop-row row 0)
(loop (+ row 1))))))
(loop 0)))
b.
(define display-table
(lambda (table)
(define show-row
(lambda (row column)
(if (= column (table-width table))
(newline)
(begin
(display (table-ref table row column))
(display " ")
(show-row row (+ column 1))))))
(define show
(lambda (row)
(if (= row (table-height table))
(newline)
(begin
(show-row row 0)
(show (+ row 1))))))
(show 0)))
Exercise 12.31: Imagine the following game: You are given a path that consists of white and black squares. The exact configuration of white and black squares varies with the game. You start on the leftmost square (which we’ll call square 0), and your goal is to move off the right end of the path in the least number of moves. However, the rules stipulate that:
If you are on a white square, you can move either 1 or 2 squares to the right.
If you are on a black square, you can move either 1 or 4 squares to the right. […]
Write a memoized version of fewest-moves.
Solution:
(define fewest-moves-mem
(lambda (path)
(let ((table (make-vector (vector-length path))))
(define fewest-moves-f
(lambda (path i)
(cond ((>= i (vector-length path))
0)
((equal? (vector-ref path i) 'white)
(+ 1 (min (fewest-moves-sub path (+ i 1))
(fewest-moves-sub path (+ i 2)))))
(else
(+ 1 (min (fewest-moves-sub path (+ i 1))
(fewest-moves-sub path (+ i 4))))))))
(define fewest-moves-sub
(lambda (path i)
(ensure-in-table! path i)
(vector-ref table i)))
(define ensure-in-table!
(lambda (path i)
(if (vector-ref table i)
'done
(store-in-table! table i))))
(define store-in-table!
(lambda (table i)
(vector-set! table i (fewest-moves path i))))
(vector-fill! table #f)
(fewest-moves-f path 0))))
Exercise 12.33: The function h(n) is defined for nonnegative integers n as follows:
a. Write a dynamic programming procedure for efficiently calculating
b. Is it possible to modify the procedure so that it stores all the values it needs in a vector of fixed size, as walk-count can be modified to store the values it needs in a two-element vector? (A vector of “fixed size” is one with a size that does not depend on the parameter, n.) Justify your answer.
Solution: a & b. I implemented b directly into the code.
(define h
(lambda (n)
(let ((vector (make-vector (+ n 1))))
(define calc-h
(lambda (n)
(cond ((< n 2) 1)
((odd? n) (+
(calc-h-sub (- n 1))
(calc-h-sub (- n 2))))
(else (+
(calc-h-sub (- n 1))
(calc-h-sub (/ n 2)))))))
(define calc-h-sub
(lambda (n)
(vector-ref vector n)))
(from-to-do 0 n
(lambda (i)
(vector-set! vector i (calc-h i))))
(calc-h n))))