Concrete Abstractions: Chapter 12

Exercise 12.4: Draw a tree, analogous to Figure 4.4 on page 92, showing how the value of C(4, 2) is computed by choose. Your tree should have C(4, 2) at the root and six 1s as its leaves.
Solution: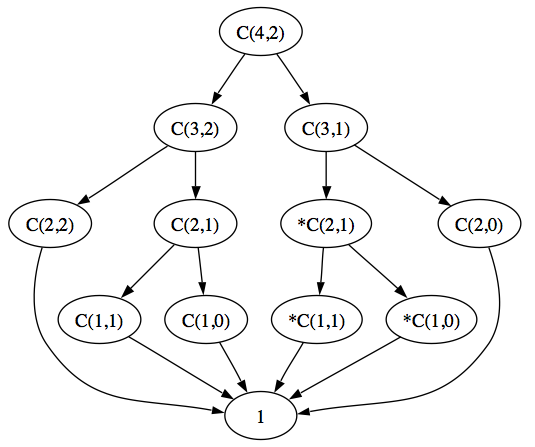

Exercise 12.6: Using these procedures, write
a. A procedure called table-fill! that takes a table and an element and sets every entry in the table to the given element. For example, (table-fill! table 0) would have a similar effect to that of zero-out-vector! in Section 11.6.
b. A procedure called display-table that nicely displays its table parameter.

Solution:

(define table-fill!
  (lambda (table value)
    (define loop-row
      (lambda (row column)
        (if (= column (table-width table))
            'done
            (begin
              (table-set! table row column value)
              (loop-row row (+ column 1))))))
    (define loop
      (lambda (row)
        (if (= row (table-height table))
            'done
            (begin
              (loop-row row 0)
              (loop (+ row 1))))))
    (loop 0)))

(define display-table
  (lambda (table)
    (define show-row
      (lambda (row column)
        (if (= column (table-width table))
            (newline)
            (begin
              (display (table-ref table row column))
              (display " ")
              (show-row row (+ column 1))))))
    (define show
      (lambda (row)
        (if (= row (table-height table))
            (newline)
            (begin
              (show-row row 0)
              (show (+ row 1))))))
    (show 0)))

Exercise 12.31: Imagine the following game: You are given a path that consists of white and black squares. The exact configuration of white and black squares varies with the game. You start on the leftmost square (which we’ll call square 0), and your goal is to move off the right end of the path in the least number of moves. However, the rules stipulate that:
If you are on a white square, you can move either 1 or 2 squares to the right.
If you are on a black square, you can move either 1 or 4 squares to the right. […]
Write a memoized version of fewest-moves.
Solution:

(define fewest-moves-mem
  (lambda (path)
    (let ((table (make-vector (vector-length path))))
      (define fewest-moves-f
        (lambda (path i)
          (cond ((>= i (vector-length path))
                 0)
                ((equal? (vector-ref path i) 'white)
                 (+ 1 (min (fewest-moves-sub path (+ i 1))
                           (fewest-moves-sub path (+ i 2)))))
                (else
                 (+ 1 (min (fewest-moves-sub path (+ i 1))
                           (fewest-moves-sub path (+ i 4))))))))

      (define fewest-moves-sub
        (lambda (path i)
          (ensure-in-table! path i)
          (vector-ref table i)))

      (define ensure-in-table!
        (lambda (path i)
          (if (vector-ref table i)
              'done
              (store-in-table! table i))))

      (define store-in-table!
        (lambda (table i)
          (vector-set! table i (fewest-moves path i))))

      (vector-fill! table #f)

      (fewest-moves-f path 0))))

Exercise 12.33: The function h(n) is defined for nonnegative integers n as follows:
$h(n) = \begin{cases} 1 & \text{ if } n<2\\ h(n-1) + h(n-2) & \text{ if n } < \text{2 and n is odd}\\ h(n-1) + h(n/2) & \text{ if n } \geq \text{2 and n is even}\\ \end{cases}$
a. Write a dynamic programming procedure for efficiently calculating $h(n).$
b. Is it possible to modify the procedure so that it stores all the values it needs in a vector of fixed size, as walk-count can be modified to store the values it needs in a two-element vector? (A vector of “fixed size” is one with a size that does not depend on the parameter, n.) Justify your answer.
Solution: a & b. I implemented b directly into the code.

(define h
  (lambda (n)
    (let ((vector (make-vector (+ n 1))))
      (define calc-h
        (lambda (n)
          (cond ((< n 2) 1)
                ((odd? n) (+
                           (calc-h-sub (- n 1))
                           (calc-h-sub (- n 2))))
                (else (+
                       (calc-h-sub (- n 1))
                       (calc-h-sub (/ n 2)))))))

      (define calc-h-sub
        (lambda (n)
          (vector-ref vector n)))

      (from-to-do 0 n
                  (lambda (i)
                    (vector-set! vector i (calc-h i))))

      (calc-h n))))

Concrete Abstractions: Chapter 10

Exercise 10.2: Even when a category is directly testable by Scheme, using EBNF to express it at a more primitive level can help you appreciate the expressive power of EBNF. In this exercise you will use EBNF to describe certain kinds of numbers—a small subset of those allowed by Scheme.
a. Write a production for <unsigned-integer>. You can use the productions for <digit> given above.
b. Next write productions for <integer>; an <integer> may start with a – sign, a + sign, or neither.
c. Finally, write productions for <real-number>, which are (possibly) signed numbers that may have a decimal point. Note that if the real number has a decimal point, there must be at least one digit to the left or to the right (or both) of the decimal point. Thus, -43., .43, 43, 43.21, and 43.0 are all valid real numbers.

Exercise 10.3: In Section 8.3 we considered expression trees for simple arithmetic expressions. All such expressions are either numbers or lists having an operator (one of +, -, *, or /) and two operands. Actually, there are three important variants, depending on where the operator occurs: in the first position (prefix or Scheme notation), the second position (infix or standard notation), or the third position (postfix, also known as Reverse Polish notation, or RPN). Let’s consider how such expressions can be specified using EBNF.
a. Write productions for <arithmetic-prefix-expression>.

b. Write productions for <arithmetic-infix-expression>.

c. Write productions for <arithmetic-postfix-expression>.

d. As noted in Section 8.3, a postorder traversal of an expression tree re-
sults in a list of the nodes that is identical to the language specified by <arithmetic-postfix-expression>, except that subexpressions are not parenthesized. Revise the productions for <arithmetic-postfix-expression> so that subexpressions are not parenthesized. (The overall top-level expression needn’t be parenthesized either.)

Solution: <arithmetic-expression> -> + | – | * | /
a. <arithmetic-prefix-expression> -> (<arithmetic-expression> <real-number> <real-number>)
b. <aritmethic-infix-expression> -> (<real-number> <arithmetic-expression> <real-number>)
c. <arithmetic-postfix-expression> -> (<real-number> <real-number> <arithmetic-expression>)

Exercise 10.4: Let’s consider two possible additions to our Micro-Scheme grammar involving regular Scheme expressions.
a. Write a production for let expressions. Remember that let expressions allow zero or more bindings (i.e., parenthesized name/expression pairs), and the body of the let contains one or more expressions. You should define a separate syntactic category for <binding>.
b. Write productions for cond expressions. Remember that cond expressions allow one or more branches, the last of which may be an else, and each branch has one or more expressions following the test condition.

Solution: a. <binding> –> (let ((<name> <expression>)) <expression>+>
b. <condition> –> (cond ((<expression>+ <expression>))+ (else <expression>+ ))

Exercise 10.6:

Solution: a. (if 3 1 5) is a <conditional>. Let’s check if 3, 1, and 5 are <expression>s. 3, 1 and 5 are <number>s which are <literal>s which are <constant>s which are <expression>s. So that’s valid.
b. (lambda x (+ x 2)) that isn’t valid because a <abstraction> needs parenthisis after lambda.
c. (((a ((b))) c)) that looks like an <application> let’s check if ((a ((b))) c) is an <expression>. Because an <application> is an <expression> we have to check if (a ((b))) and c is an <expression>. c is an <name> and therefore an <expression>. (a ((b))) is an <application> which have to consists of one or more expressions. So there’s a ((b)) left to check. a is an <expression>. ((b)) is an <application> of an <application> of a <name> which is an <expression>. So that’s valid.
d. (lambda (lambda) 3). We have to check if lambda ist a <name> which is false. Not valid.
e. (lambda () lambda). We have to check if lambda is an <expression> which it isn’t.
f. (lambda (x) (if (> x 0) x (- x) 0)). Let’s check if if is an <conditional>. It isn’t because it has more than three <expression>s in its body.
g. (lambda () x). This is valid if x is an <expression>. A <name> is an <expression>, so this is valid.
h. (lambda () ). Not valid, because there’s no <expression> in the body.
i. (/). Not valid, because it needs at least two <arithmetic-expression>s in the body.
j. (#t #f). This is an <application> of two expressions. Are #f and #t <expression>s? They aren’t definied, so this is not valid.

Exercise 10.31: Use EBNF to write a grammar for the language of all strings of one or more digits that simultaneously meet both of the following requirements:
a. The digits alternate between even and odd, starting with either.

b. The string of digits is the same backward as forward (i.e., is palindromic).

Solution:

<even> -> 0 | 2 | 4 | 6 | 8
<odd>  -> 1 | 3 | 5 | 7 | 9
<palindrome-even> -> 0<palindrome-odd>0 | 2<palindrome-odd>2 | 4<palindrome-odd>4 | 6<palindrome-odd>6 |
                     8<palindrome-odd>8 | <even>
<palindrome-odd> ->  1<palindrome-even>1 | 3<palindrome-even>3 | 5<palindrome-even>5 | 7<palindrome-even>7 | 
                     9<palindrome-even>9 | <odd>
<legal> -> <palindrome-even> | <palindrome-odd>

Concrete Abstractions: Chapter 9

Exercise 9.2: The sequences we just described are restricted to consecutive increasing sequences of integers (more precisely, to increasing arithmetic sequences where consecutive elements differ by 1). We can easily imagine similar but more general sequences such as <6, 4, 3, 2> or <5, 5.1, 5.2, 5.3, 5.4, 5.5>—in other words, general arithmetic sequences of a given length, starting value, and increment (with decreasing sequences having a negative increment value).
a. Write a procedure sequence-with-from-by that takes as arguments a length, a starting value, and an increment and returns the corresponding arithmetic sequence. Thus, (sequence-with-from-by 5 6 -1) would return the first and (sequence-with-from-by 6 5 .1) would return the second of the two pre- ceding sequences. Remember that sequences are represented as procedures, so your new sequence constructor will need to produce a procedural result.
b. The procedure sequence-from-to can now be rewritten as a simple call to sequence-with-from-by. The original sequence-from-to procedure made an empty sequence if its first argument was greater than its second, but you should make the new version so that you can get both increasing and de- creasing sequences of consecutive integers. Thus, (sequence-from-to 3 8) should return <3, 4, 5, 6, 7, 8>, whereas (sequence-from-to 5 1) should return <5, 4, 3, 2, 1>.
c. Write a procedure sequence-from-to-with that takes a starting value, an ending value, and a length and returns the corresponding arithmetic sequence. For example, (sequence-from-to-with 5 11 4) should return <5, 7, 9, 11>.

Solution:

; a.
(define sequence-with-from-by
  (lambda (start len inc)
    (lambda (op)
      (cond ((equal? op 'empty-sequence?)
              (= len 0))
            ((equal? op 'head)
               start)
            ((equal? op 'tail)
               (sequence-with-from-by (+ start inc) (- len 1) inc))
            ((equal? op 'sequence-length)
               len)
            (else
               (error "illegal operation" op))))))

; b.
(define sequence-from-to
  (lambda (a b)
    (if (< a b)
      (sequence-with-from-by a (+ (- b a) 1) 1)
      (sequence-with-from-by a (+ (- a b) 1) (- 1)))))

; c.
(define sequence-from-to-with
  (lambda (start end len)
   (sequence-with-from-by start len (/ (+ (- end start) 2) len))))

Exercise 9.6: Write the sequence constructor sequence-map, that outwardly acts like the list procedure map. However unlike map, which applies the procedural argument to all the list elements, sequence-map should not apply the procedural argument at all yet. Instead, when an element of the resulting sequence (such as its head) is accessed, that is when the procedural argument should be applied.

Solution:

(define sequence-map
  (lambda (sequence f)
   (lambda (op)
     (cond
       ((equal? op 'empty-sequence?)
         (empty-sequence? sequence))
       ((equal? op 'head)
         (f (head sequence)))
       ((equal? op 'tail)
         (sequence-map (tail sequence) f))
       ((equal? op 'sequence-length)
         new-length)
       ((equal? op 'sequence-ref)
        (lambda (n)
         (if (= n 0)
           head
           (sequence-ref tail (- n 1)))))
       (else (error "illegal sequence operation" op))))))

Exercise 9.: One way we can represent a set is as a predicate (i.e., a procedure that returns true or false). The idea is that to test whether a particular item is in the set, we pass it to the procedure, which provides the answer. For example, using this representation, the built-in procedure number? could be used to represent the (infinite) set of all numbers.
a. Implement element-of-set? for this representation. It takes two arguments, an element and a set, and returns true or false depending on whether the element is in the set or not.
b. Implement add-to-set for this representation. It takes two arguments, an ele- ment and a set, and returns a new set that contains the specified element as well as everything the specified set contained. Hint: Remember that a set is represented as a procedure.
c. Implement union-set for this representation. It takes two arguments—two sets— and returns a new set that contains anything that either of the provided sets contains.

Solution:

; a
(define element-of-set?
  (lambda (element set)
   (set element)))

; b.
(define add-to-set
  (lambda (element set)
    (lambda (ele)
      (if (equal? ele element)
        #t
        (set ele)))))

; c.
(define union-set
  (lambda (set1 set2)
    (lambda (ele)
      (or (set1 ele) (set2 ele)))))

Exercise 9.: Assume that infinity has been defined as a special number that is greater than all normal (finite) numbers and that when added to any finite number or to itself, it yields itself. Now there is no reason why sequences need to be of finite length. Write a constructor for some interesting kind of infinite sequence.

Solution:

; Ex 9.22
(define sequence-from-to-inf
  (lambda (from)
    (lambda (op)
     (cond ((equal? op 'head)
        from)
           ((equal? op 'tail)
        (sequence-from-to-inf (+ 1 from)))
           ((equal? op 'sequence-length)
         +inf.0)
           (else
         (error "operation not found" op))))))</code>

; Interesting application
(define display-even-sequence
  (lambda (seq)
    (if (even? (head seq))
        (display (head seq))
        (display " "))
        (display-even-sequence (tail seq))))

(define display-f-sequence
  (lambda (seq f)
    (display (f (head seq)))
    (display " ")
    (display-f-sequence (tail seq) f)))

Concrete Abstractions: Chapter 8

Exercise 8.1: Write a procedure called minimum that will find the smallest element in a nonempty binary search tree of numbers.

Solution:

(define minimum
  (lambda (tree)
    (if (empty-tree? (left-subtree tree))
        (root tree)
        (minimum (left-subtree tree)))))

Exercise 8.2: Write a procedure called number-of-nodes that will count the number of elements in a binary search tree.

Solution:

(define number-of-nodes
  (lambda (tree)
    (if (empty-tree? tree)
        0
        (+ 1 
           (number-of-nodes (left-subtree tree))
           (number-of-nodes (right-subtree tree))))))

Exercise 8.6: Suppose we want to create a new binary search tree by adding another element to an already existing binary search tree. Where is the easiest place to add such an element? Write a procedure called insert that takes a number and a binary search tree of numbers and returns a new binary search tree whose elements consist of the given number together with all of the elements of the binary search tree. You may assume that the given number isn’t already in the tree.

Solution:

(define insert
  (lambda (tree x)
    (if (empty-tree? tree)
        (make-nonempty-tree x '() '())
    (cond ((< x (root tree))
           (make-nonempty-tree 
            (root tree) (insert (left-subtree tree) x) (right-subtree tree)))
          ((> x (root tree))
           (make-nonempty-tree
            (root tree ) (left-subtree tree) (insert (right-subtree tree) x)))))))

Exercise 8.7: Using the procedure insert, write a procedure called list->bstree that takes a list of numbers and returns a binary tree whose elements are those numbers. Try this on several different lists and draw the corresponding tree diagrams. What kind of list gives you a short bushy tree? What kind of list gives a tall skinny tree?

Solution:

(define list->bstree
  (lambda (lst)
    (if (null? lst)
        (make-empty-tree)
        (insert (list->bstree (cdr lst)) (car lst)))))

Exercise 8.11: In many applications, binary trees aren’t sufficient because we need more than two subtrees. An m-ary tree is a tree that is either empty or has a root and m subtrees, each of which is an m-ary tree. Generalize the previous results to m-ary trees.

Solution:
Ok. So let’s see if we can find a formular for 3-ary trees first.

So we can see that a tree with an height of two has $3^2 + 3^1 + 3^0$ nodes. Or more general: A 3-ary tree with an height of n has $sum_{i=0}^{n} 3^i$ nodes. This can be simplified as $frac{1 - 3^{n+1}}{1-3}.$ So is this true? Let’s see. The height should be n. What’s happening if we increase the height by one? Each leave will get three children. We assumed that there are $3^n$ leaves. Therefore there will be $3^n * 3 = 3^{n+1}$ children. That is, there will be at most $text{nodes}(n+1) = text{nodes}(n) + 3^{n+1}$ nodes which is equivalent to $sum_{i=0}^{n} 3^i + 3^{n+1} = sum_{i=0}^{n+1} 3^i.$
Therefore there are $sum_{i=0}^{n} m^i$ nodes in a m-ary of height n.

Exercise 8.12: In Exercise 8.7, you wrote a procedure list->bstree that created a binary search tree from a list by successively inserting the elements into the tree. This procedure can lead to trees that are far from minimum height—surprisingly, the worst case occurs if the list is in sorted order. However, if you know the list is already in sorted order, you can do much better: Write a procedure sorted-list->min-height-bstree that creates a minimum height binary search tree from a sorted list of numbers. Hint: If the list has more than one element, split it into three parts: the middle element, the elements before the middle element, and the elements after. Construct the whole tree by making the appropriate recursive calls on these sublists and combining the results.

Solution:

(define sorted-list->min-height-bstree
  (lambda (lst)
    (if (null? lst)
        (make-empty-tree)
        (if (not (list? lst))
            lst
            (make-nonempty-tree (middle-item lst) 
                                (sorted-list->min-height-bstree (left-items lst)) 
                                (sorted-list->min-height-bstree (right-items lst)))))))


(define list-element-range
  (lambda (lst start end i)
    (if (null? lst)
        '()
        (cond ((> i end)
               '())
              ((= i end)
               (cons (car lst) (list-element-range '() start end (+ i 1))))
              ((or (= i start) (> i start))
               (cons (car lst) (list-element-range (cdr lst) start end (+ i 1))))
              (else
               (list-element-range (cdr lst) start end (+ i 1)))))))

(define middle-item
  (lambda (lst)
    (let ((len (length lst)))
      (if (even? len)
        (list-element-range lst (/ len 2) (/ len 2) 0)
        (list-element-range lst (- (/ (+ len 1) 2) 1) (- (/ (+ len 1) 2) 1) 0)))))

(define left-items
  (lambda (lst)
    (let ((len (length lst)))
          (if (even? len)
              (list-element-range lst 0 (- (/ len 2) 1) 0)
              (list-element-range lst 0 (- (/ (+ len 1) 2) 2) 0)))))

(define right-items
  (lambda (lst)
    (let ((len (length lst)))
          (if (even? len)
              (list-element-range lst (+ 1 (/ len 2)) (+ len 1) 0)
              (list-element-range lst (/ (+ len 1) 2) len 0)))))

Exercise 8.31: Write a procedure that takes as arguments a binary search tree of numbers, a lower bound, and an upper bound and counts how many elements of the tree are greater than or equal to the lower bound and less than or equal to the upper bound. Assume that the tree may contain duplicate elements. Make sure your procedure doesn’t examine more of the tree than is necessary.

Solution:

(define count-elements-in-boundary
   (lambda (tree lower upper)
     (if (empty-tree? tree)
         0
         (+ 
          (if (or (< (root tree) lower) (> (root tree) upper))
             0
             1) 
          (count-elements-in-boundary (left-subtree tree) lower upper)
          (count-elements-in-boundary (right-subtree tree) lower upper)))))