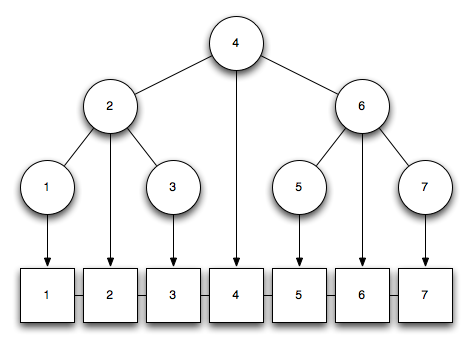
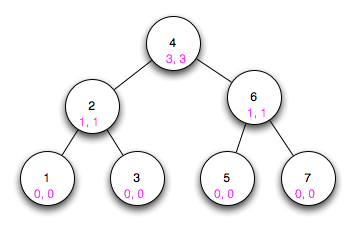
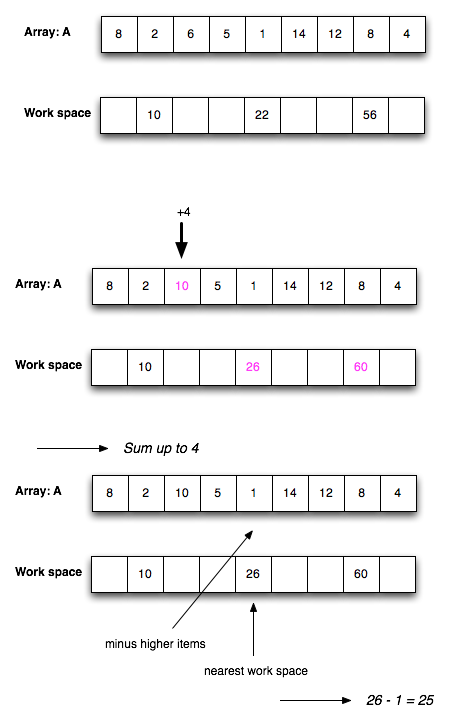
4-1. The Grinch is given the job of partitioning 2n players into two teams of n players each. Each player has a numerical rating that measures how good he/she is at the game. He seeks to divide the players as unfairly as possible, so as to create the biggest possible talent imbalance between team A and team B. Show how the Grinch can do the job in 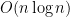 time.
time.
Solution First sort the players with an algorithm which runs in 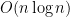 time and afterwards form two teams with the first n player in the first team and the last n players in the second team.
time and afterwards form two teams with the first n player in the first team and the last n players in the second team.
4-3. Take a sequence of 2n real numbers as input.Design an 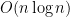 algorithm that partitions the numbers into n pairs, with the property that the partition minimizes the maximum sum of a pair. For example, say we are given the numbers (1,3,5,9). The possible partitions are ((1,3),(5,9)), ((1,5),(3,9)), and ((1,9),(3,5)). The pair sums for these partitions are (4,14), (6,12), and (10,8). Thus the third partition has 10 as its maximum sum, which is the minimum over the three partitions.
algorithm that partitions the numbers into n pairs, with the property that the partition minimizes the maximum sum of a pair. For example, say we are given the numbers (1,3,5,9). The possible partitions are ((1,3),(5,9)), ((1,5),(3,9)), and ((1,9),(3,5)). The pair sums for these partitions are (4,14), (6,12), and (10,8). Thus the third partition has 10 as its maximum sum, which is the minimum over the three partitions.
Solution We can minimize the maximum sum if we pair up the lowest and the highest element. But first we have to sort our numbers which takes  and create the pairs which takes
and create the pairs which takes 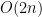 .
.
Let S be the sequence with length 2n
sort S
for i := 1 to n
pair[i] = (S[i], S[2n - i - 1])
4-6. Given two sets 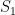 and
and  (each of size n), and a number x, describe an
(each of size n), and a number x, describe an 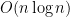 algorithm for finding whether there exists a pair of elements, one from
algorithm for finding whether there exists a pair of elements, one from 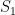 and one from
and one from  , that add up to x. (For partial credit, give a
, that add up to x. (For partial credit, give a  algorithm for this problem.)
algorithm for this problem.)
Solution We could sort  and then iterate through
and then iterate through 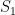 and calculate the second number
and calculate the second number 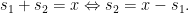 Now we just have to search for
Now we just have to search for  in
in  which takes
which takes 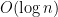 time. Therefore we take
time. Therefore we take  time.
time.
4-7. Outline a reasonable method of solving each of the following problems. Give the order of the worst-case complexity of your methods.
(a) You are given a pile of thousands of telephone bills and thousands of checks sent in to pay the bills. Find out who did not pay.
(b) You are given a list containing the title, author, call number and publisher of all the books in a school library and another list of 30 publishers. Find out how many of the books in the library were published by each company.
(c) You are given all the book checkout cards used in the campus library during the past year, each of which contains the name of the person who took out the book. Determine how many distinct people checked out at least one book.
Solution (a) We can use quick sort in this scenario which works in expected 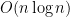 time and match the ith bill with the ith check which takes
time and match the ith bill with the ith check which takes  time.
time.
(b) We can use a dictionary quite easily which counts the books by publisher. This takes 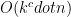 where
where  time.
time.
(c) We can sort the list by name and then iterate through it and count each different name. This takes about  time.
time.
4-9. Give an efficient algorithm to compute the union of sets A and B, where  The output should be an array of distinct elements that form the union of the sets, such that they appear more than once in the union.
The output should be an array of distinct elements that form the union of the sets, such that they appear more than once in the union.
(a) Assume that A and B are unsorted. Give an 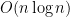 algorithm for the problem.
algorithm for the problem.
(b) Assume that A and B are sorted. Give an O(n) algorithm for the problem.
Solution (a) We can create one array with every element of A and B. Afterwards we sort this array and iterate through it. In this iteration we just have to check if ith item differs from the (i+1)th item which takes  therefore we need
therefore we need 
(b)
Let A got n elements and B got m elements with n >= m.
i := 1 # counter for A, A[1] is first element
j := 1 # counter for B
while i <= n
if j >= m # no more elements in B
add A[i] to union set
i := i + 1
else if A[i] == B[j] # same element
add A[i] to union set
i := i + 1
j := j + 1
else if A[i] > B[j] # increase j until B[j] is big enough
add B[j] to union set
j := j + 1
else if A[i] < B[j]
add A[j] to union set
i := i + 1
4-12. Devise an algorithm for finding the k smallest elements of an unsorted set of n integers in 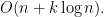
Solution We can build an “unsorted” heap in  , i.e. only bring the smallest item at the top. Now we can extract k times the smallest item which takes $O(k \log n)$ time.
, i.e. only bring the smallest item at the top. Now we can extract k times the smallest item which takes $O(k \log n)$ time.
4-13. You wish to store a set of n numbers in either a max-heap or a sorted array. For each application below, state which data structure is better, or if it does not matter. Explain your answers.
(a) Want to find the maximum element quickly.
(b) Want to be able to delete an element quickly.
(c) Want to be able to form the structure quickly.
(d) Want to find the minimum element quickly.
Solution (a) They are both equally fast. In the max-heap it’s the first element in the sorted array the last one.
(b) A max-heap is here better because it takes only 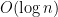 instead of
instead of  for a sorted array.
for a sorted array.
(c) Both the heap and the sorted array take 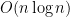 time to be formed.
time to be formed.
(d) The minimum element in a sorted array is the first. In a max-heap every leaf could be the minimum element, therefore it takes 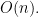
4-14. Give an  -time algorithm that merges k sorted lists with a total of n elements into one sorted list. (Hint: use a heap to speed up the elementary
-time algorithm that merges k sorted lists with a total of n elements into one sorted list. (Hint: use a heap to speed up the elementary  – time algorithm).
– time algorithm).
Solution We can basically do an heap sort on these lists. We iterate from i := 1 to n and select the smallest item from the head of each list which takes  time. Therefore the algorithm takes
time. Therefore the algorithm takes 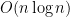 time.
time.
4-15. (a) Give an efficient algorithm to find the second-largest key among n keys. You can do better than 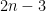 comparisons.
comparisons.
(b) Then, give an efficient algorithm to find the third-largest key among n keys. How many key comparisons does your algorithm do in the worst case? Must your algorithm determine which key is largest and second-largest in the process?
Solution (a) There’s a faster method for construction heaps which runs in  . Afterwards we just have to call find-min two times which takes
. Afterwards we just have to call find-min two times which takes 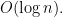
(b) We can use the same method here as well. The largest second-largest key is implicitly found by constructing the heap.
4-16. Use the partitioning idea of quicksort to give an algorithm that finds the median element of an array of n integers in expected  time.
time.
Solution The partition part of quicksort basically can help us. It determines partitions which are bigger respectively smaller than the pivot element. We just have to find n/2 elements which are smaller or equal to our element m which is then the median. This takes expected  time.
time.
4-19. An inversion of a permutation is a pair of elements that are out of order.
(a) Show that a permutation of n items has at most 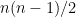 inversions. Which permutation(s) have exactly
inversions. Which permutation(s) have exactly 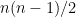 inversions?
inversions?
(b) Let P be a permutation and Pr be the reversal of this permutation. Show that 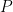 and
and  have a total of exactly
have a total of exactly 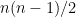 inversions.
inversions.
(c) Use the previous result to argue that the expected number of inversions in a random permutation is 
Solution (a) Let’s take for example the items 1..5. We can get the maximum inversions if we reverse this list, i.e. [5, 4, 3, 2, 1] or more general [n, n-1, …, 1]. Now we can start at the right and count the inversions.

Sublist Inversions #Inversions
1 0
2, 1 (2,1) 1
3, 2, 1 (3, 2), (3, 1) 2
4, 3, 2, 1 (4, 3), (4, 2), (4, 1) 3
5, 4, 3, 2, 1 (5, 4), (5, 3), (5, 2), (5,1) 4
Therefore we got  inversions at most.
inversions at most.
(b) Let’s prove this relation. Assume we got a permutation with n items. Let’s add an other item. The reversal for the old permutation got 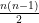 inversions. The (n+1)th item adds n inversions which are:
inversions. The (n+1)th item adds n inversions which are:
 Therefore we get
Therefore we get 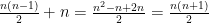 and we’re done.
and we’re done.
(c) A rough approach is to take the smallest and the highest value and assume that inversions are uniformly distribute. Therefore we get 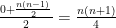
4-24. Let A[1..n] be an array such that the first 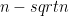 elements are already sorted (though we know nothing about the remaining elements). Give an algorithm that sorts A in substantially better than
elements are already sorted (though we know nothing about the remaining elements). Give an algorithm that sorts A in substantially better than 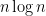 steps.
steps.
Solution Merge sort can used quite nicely. We need to sort the remaining 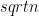 which takes
which takes 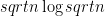 time. Afterwards we have to use merge on our old and new sorted lists which takes
time. Afterwards we have to use merge on our old and new sorted lists which takes  time.
time.
4-29. Mr. B. C. Dull claims to have developed a new data structure for priority queues that supports the operations Insert, Maximum, and Extract-Max—all in 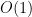 worst-case time. Prove that he is mistaken. (Hint: the argument does not involve a lot of gory details—just think about what this would imply about the
worst-case time. Prove that he is mistaken. (Hint: the argument does not involve a lot of gory details—just think about what this would imply about the  lower bound for sorting.)
lower bound for sorting.)
Solution If insert, maximum and extract-max would be possible in 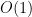 we could use the following algorithm to sort data.
we could use the following algorithm to sort data.
A[1...n]
for i := 1 to n
insert(A[i])
for i := 1 to n
A[i] = maximum()
Extract-max()
This would sort data in  which is smaller than lower bound
which is smaller than lower bound 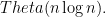
4-30. A company database consists of 10,000 sorted names, 40% of whom are known as good customers and who together account for 60% of the accesses to the database. There are two data structure options to consider for representing the database:
• Put all the names in a single array and use binary search.
• Put the good customers in one array and the rest of them in a second array. Only if we do not find the query name on a binary search of the first array do we do a binary search of the second array.
Demonstrate which option gives better expected performance. Does this change if linear search on an unsorted array is used instead of binary search for both options?
Solution Single array, binary search: 
Good and bad, binary search: 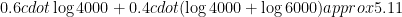
The first variant is a bit faster here.
Single array, unsorted: 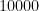
Good and bad, unsorted: 
However in this case the second variant is far superior.
4-32. Consider the numerical 20 Questions game. In this game, Player 1 thinks of a number in the range 1 to n. Player 2 has to figure out this number by asking the fewest number of true/false questions. Assume that nobody cheats.
(a) What is an optimal strategy if n in known?
(b) What is a good strategy is n is not known?
Solution (a) Binary search.
(b) We can start asking if the number is between 1 and two. If not we can double our range from two to four, four and eight, etc.
4-35. Let M be an 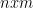 integer matrix in which the entries of each row are sorted in increasing order (from left to right) and the entries in each column are in increasing order (from top to bottom). Give an efficient algorithm to find the position of an integer x in M, or to determine that x is not there. How many comparisons of x with matrix entries does your algorithm use in worst case?
integer matrix in which the entries of each row are sorted in increasing order (from left to right) and the entries in each column are in increasing order (from top to bottom). Give an efficient algorithm to find the position of an integer x in M, or to determine that x is not there. How many comparisons of x with matrix entries does your algorithm use in worst case?
Solution
for j:= 1 to m
if m[1][j] <= x <= m[n][j]
do binary search on this row
if found return value
return Not found
This algorithm runs in  time.
time.
4-39. Design and implement a parallel sorting algorithm that distributes data across several processors. An appropriate variation of mergesort is a likely candidate. Mea- sure the speedup of this algorithm as the number of processors increases. Later, compare the execution time to that of a purely sequential mergesort implementation. What are your experiences?
Solution Non-threaded version:
from random import randint
def mergesort(lst):
n = len(lst)
if n < 2:
return lst
else:
middle = n / 2
left = mergesort(lst[:middle])
right = mergesort(lst[middle:])
return merge(left, right)
def merge(left, right):
result = []
i = 0
j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:] # append the rest
result += right[j:]
return result
unsorted = [randint(0, 150000) for i in xrange(0, 10 ** 6)]
mergesort(unsorted)
Threaded version:
from random import randint
from multiprocessing import Process, Queue
def mergesort(lst):
n = len(lst)
if n < 2:
return lst
else:
middle = n / 2
left = mergesort(lst[:middle])
right = mergesort(lst[middle:])
return merge(left, right)
def merge(left, right):
result = []
i = 0
j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result += left[i:] # append the rest
result += right[j:]
return result
def callMergesort(lst, q):
q.put(mergesort(lst))
def main():
unsorted = [randint(0, 150000) for i in xrange(0, 10 ** 6)]
middle = 5 * 10 ** 5
q = Queue()
p1 = Process(target = callMergesort, args = (unsorted[:middle], q))
p2 = Process(target = callMergesort, args = (unsorted[middle:], q))
p1.start()
p2.start()
merge(q.get(), q.get())
if __name__ == '__main__':
main()
For small to medium sizes the threaded version is a bit slower than the non-threaded one. However, for very big sizes the threaded version works faster.
4-45. Given a search string of three words, find the smallest snippet of the document that contains all three of the search words—i.e. , the snippet with smallest number of words in it. You are given the index positions where these words in occur search strings, such as word1: (1, 4, 5), word2: (4, 9, 10), and word3: (5, 6, 15). Each of the lists are in sorted order, as above.
Solution We can sort these positions with its identifier. Afterwards we iterative through the list and put identifiers on a stack. If we got all of them, we found the snippet. We replace each identifier if we find a nearer one. At the end, we just have to search for the smallest snippet in all snippets.