3-1. A common problem for compilers and text editors is determining whether the parentheses in a string are balanced and properly nested. For example, the string ((())())() contains properly nested pairs of parentheses, which the strings )()( and ()) do not. Give an algorithm that returns true if a string contains properly nested and balanced parentheses, and false if otherwise. For full credit, identify the position of the first offending parenthesis if the string is not properly nested and balanced.
Solution:
def isBalanced(lst):
stack = []
for position, item in enumerate(lst):
if item == "(":
stack.append((item, position))
else:
if stack != []: # no more open parentheses
stack.pop() # pops "("
else:
return (False, position)
if stack == []:
return True
else:
return (False, stack[0][1])
print ")()( :", isBalanced(list(")()("))
print "()) :", isBalanced(list("())"))
print "((()()))() :", isBalanced(list("((()()))()"))
print "(())(())()()()()(() :", isBalanced(list("(())(())()()()()(()"))
3-3. We have seen how dynamic arrays enable arrays to grow while still achieving constant-time amortized performance. This problem concerns extending dynamic arrays to let them both grow and shrink on demand.
(a) Consider an underflow strategy that cuts the array size in half whenever the array falls below half full. Give an example sequence of insertions and deletions where this strategy gives a bad amortized cost.
(b) Then, give a better underflow strategy than that suggested above, one that achieves constant amortized cost per deletion.
Solution: 3-3. (a) Let’s assume that the array is current fulled at half. If we delete one element it will cut in half. If we now add a new element it have to expand.
(b) Instead of shrinking it by half its size I would shrink it only by a forth its size. So we have a buffer which avoids shrinking and expanding in too short periods.
3-4. Design a dictionary data structure in which search, insertion, and deletion can all be processed in O(1) time in the worst case. You may assume the set elements are integers drawn from a finite set 1, 2, .., n, and initialization can take O(n) time.
Solution: Luckily these are sets so there are no duplicates. Therefore we can use an array with size n. It takes to fill the array. Search (A[i]) can be done in
, also insertion (A[i] = v). To remove data we can just use a specific value like NUL which works also in
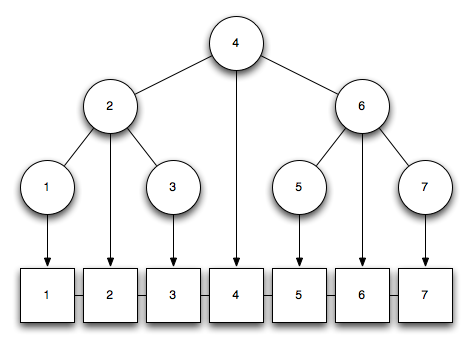
3-6. Describe how to modify any balanced tree data structure such that search, insert, delete, minimum, and maximum still take O(\log n) time each, but successor and predecessor now take O(1) time each. Which operations have to be modified to support this?
Solution: My idea is to take a search tree and use a double linked list for the predecessors and successors. You can see how this works in this picture:
Each node gets a pointer to its entry on the double linked list. Let’s see if it still works in . Search, minimum and maximum haven’t really changed, so this works still fine. What about insert and delete? Assume that 3 isn’t inserted yet. We transverse the list up to node 2. We know that the node of 3 will be placed on the right. Now we have to check what happens with the double linked list.
Node 2 refers to list entry 2 which has a successor list entry 4. So we have to point 2 to 3 and 3 to 2 and 4 and we’re done. The same works for deletion. Successor and predecessor are available through the double linked list with . And we’re done.
3-8. Design a data structure to support the following operations:
• insert(x,T) – Insert item x into the set T .
• delete(k,T) – Delete the kth smallest element from T.
• member(x,T) – Return true iff x ∈ T .
All operations must take time on an n-element set.
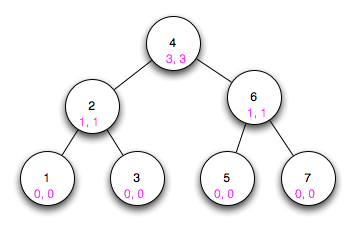
Solution: We use a basic binary search tree for this and add two counters which count the number of children nodes.
Here you can see how the counters in pink. Let’s look at 4. The pink 2 indicates that there are 2 nodes on the left, i.e. smaller than 4. And the pink 3 indicates that there are 3 nodes on the right, i.e. bigger than 4. What happens if we insert an item?
We do the standard insert traversal of a binary search tree with the difference that in each node we add a one to our counter because there will be one more node if we added our new item.
You can see what happened when we added 1. Besides adding the node we increased the left counter of 2 by one and the left counter by 4 by 1 because we traveled this way. So there’s no problem on inserting new nodes with complexity.
The next method is member which is basically search in a binary search tree which also works with a complexity of
The last one is delete(k, T) which removes the kth smallest item. Finally we can use our counters. The first counter indicates if our kth smallest item is on the left, the item or on the right.
Example 1: We want the 3th smallest item. We start at 4 and see that there are 3 items on the left, i.e. the 3th smallest item in its left children. Next we are at 2 and see that there are 1 on the left and 1 on the right, therefore we have to go right (1 left + item itself + 1 right item = 3). Now we have arrived 3 and there are no other child items therefore 3 is our 3th smallest item.
Example 2: We want the 4th smallest item. We start at 4 and see that there are 3 items to the left. Therefore the 4th smallest item is 4 itself.
This is basically some kind of binary search so it also works with complexity.
3-12. Suppose you are given an input set S of n numbers, and a black box that if given any sequence of real numbers and an integer k instantly and correctly answers whether there is a subset of input sequence whose sum is exactly k. Show how to use the black box O(n) times to find a subset of S that adds up to k.
Solution: The first time we enter our set S. If it returns yes we can continue otherwise it isn’t possible to form the sequence which sums up to k.
The next step is to test our Set without the first element. If the black box returns yes we can delete it from our set otherwise we know that it is needed. We do this for each element and our S shrinks to a set which sums up to k.
3-13. Let A[1..n] be an array of real numbers. Design an algorithm to perform any sequence of the following operations:
• Add(i,y) – Add the value y to the ith number.
• Partial-sum(i) – Return the sum of the first i numbers, i.e.
There are no insertions or deletions; the only change is to the values of the numbers. Each operation should take steps. You may use one additional array of size n as a work space.
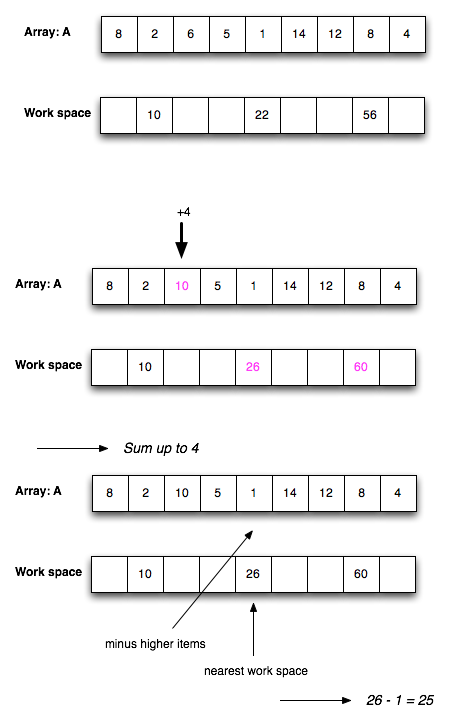
Solution: The general idea is to use the work space for the sums. Instead of using each i, I will only use log n of them to guarantee for each operation.
function Add(i, y)
A[i] = A[i] + y
for each workspace with index j
workspace[j] = workspace[j] + 1
This function takes time.
function Partial-sum(i)
find nearest workspace
sum = 0
if nearest workspace index > needed \sum index
substract numbers from nearest workspace to \sum
else
add numbers with nearest workspace to \sum
return sum
Here you can see how this works on an example:
3-17. A Caesar shift (see Section 18.6 (page 641)) is a very simple class of ciphers for secret messages. Unfortunately, they can be broken using statistical properties of English. Develop a program capable of decrypting Caesar shifts of sufficiently long texts.
Solution:
def countChars(s):
myCount = dict()
s = s.upper() # don't have to distingush between upper and lower case
for c in s:
if c == " " or c == "n":
continue
if c in myCount.keys():
myCount[c] += 1
else:
myCount[c] = 1
return myCount
def deCaesar(s):
letterProb = { 'A': 8.167 * 0.01,
'B': 1.492 * 0.01,
'C': 2.782 * 0.01,
'D': 4.253 * 0.01,
'E': 12.702 * 0.01,
'F': 2.228 * 0.01,
'G': 2.015 * 0.01,
'H': 6.094 * 0.01,
'I': 6.966 * 0.01,
'J': 0.153 * 0.01,
'K': 0.772 * 0.01,
'L': 4.025 * 0.01,
'M': 2.406 * 0.01,
'N': 6.749 * 0.01,
'O': 7.507 * 0.01,
'P': 1.929 * 0.01,
'Q': 0.095 * 0.01,
'R': 5.987 * 0.01,
'S': 6.327 * 0.01,
'T': 9.056 * 0.01,
'U': 2.758 * 0.01,
'V': 0.978 * 0.01,
'W': 2.360 * 0.01,
'X': 0.150 * 0.01,
'Y': 1.974 * 0.01,
'Z': 0.074 * 0.01}
counts = countChars(s)
countsSorted = sorted(counts.iteritems(), key = lambda (k, v) : (v, k),
reverse = True)
letterProbSorted = sorted(letterProb.iteritems(), key = lambda (k, v) : (v, k),
reverse = True)
firstCount = countsSorted[0][0]
firstLetter = letterProbSorted[0][0]
return ord(firstCount) - ord(firstLetter)
txt = """UHVHDUFKHUV (EORRP (1985), EUBDQ & KDUWHU (1899), KDBHV (1989), VLPPRQ & FKDVH (1973)) KDYH VKRZQ LW WDNHV DERXW WHQ BHDUV WR GHYHORS HASHUWLVH LQ DQB RI D ZLGH YDULHWB RI DUHDV, LQFOXGLQJ FKHVV SODBLQJ, PXVLF FRPSRVLWLRQ, WHOHJUDSK RSHUDWLRQ, SDLQWLQJ, SLDQR SODBLQJ, VZLPPLQJ, WHQQLV, DQG UHVHDUFK LQ QHXURSVBFKRORJB DQG WRSRORJB. WKH NHB LV GHOLEHUDWLYH SUDFWLFH: QRW MXVW GRLQJ LW DJDLQ DQG DJDLQ, EXW FKDOOHQJLQJ BRXUVHOI ZLWK D WDVN WKDW LV MXVW EHBRQG BRXU FXUUHQW DELOLWB, WUBLQJ LW, DQDOBCLQJ BRXU SHUIRUPDQFH ZKLOH DQG DIWHU GRLQJ LW, DQG FRUUHFWLQJ DQB PLVWDNHV. WKHQ UHSHDW. DQG UHSHDW DJDLQ. WKHUH DSSHDU WR EH QR UHDO VKRUWFXWV: HYHQ PRCDUW, ZKR ZDV D PXVLFDO SURGLJB DW DJH 4, WRRN 13 PRUH BHDUV EHIRUH KH EHJDQ WR SURGXFH ZRUOG-FODVV PXVLF. LQ DQRWKHU JHQUH, WKH EHDWOHV VHHPHG WR EXUVW RQWR WKH VFHQH ZLWK D VWULQJ RI #1 KLWV DQG DQ DSSHDUDQFH RQ WKH HG VXOOLYDQ VKRZ LQ 1964. EXW WKHB KDG EHHQ SODBLQJ VPDOO FOXEV LQ OLYHUSRRO DQG KDPEXUJ VLQFH 1957, DQG ZKLOH WKHB KDG PDVV DSSHDO HDUOB RQ, WKHLU ILUVW JUHDW FULWLFDO VXFFHVV, VJW. SHSSHUV, ZDV UHOHDVHG LQ 1967. PDOFROP JODGZHOO UHSRUWV WKDW D VWXGB RI VWXGHQWV DW WKH EHUOLQ DFDGHPB RI PXVLF FRPSDUHG WKH WRS, PLGGOH, DQG ERWWRP WKLUG RI WKH FODVV DQG DVNHG WKHP KRZ PXFK WKHB KDG SUDFWLFHG:
HYHUBRQH, IURP DOO WKUHH JURXSV, VWDUWHG SODBLQJ DW URXJKOB WKH VDPH WLPH - DURXQG WKH DJH RI ILYH. LQ WKRVH ILUVW IHZ BHDUV, HYHUBRQH SUDFWLVHG URXJKOB WKH VDPH DPRXQW - DERXW WZR RU WKUHH KRXUV D ZHHN. EXW DURXQG WKH DJH RI HLJKW UHDO GLIIHUHQFHV VWDUWHG WR HPHUJH. WKH VWXGHQWV ZKR ZRXOG HQG XS DV WKH EHVW LQ WKHLU FODVV EHJDQ WR SUDFWLVH PRUH WKDQ HYHUBRQH HOVH: VLA KRXUV D ZHHN EB DJH QLQH, HLJKW EB DJH 12, 16 D ZHHN EB DJH 14, DQG XS DQG XS, XQWLO EB WKH DJH RI 20 WKHB ZHUH SUDFWLVLQJ ZHOO RYHU 30 KRXUV D ZHHN. EB WKH DJH RI 20, WKH HOLWH SHUIRUPHUV KDG DOO WRWDOOHG 10,000 KRXUV RI SUDFWLFH RYHU WKH FRXUVH RI WKHLU OLYHV. WKH PHUHOB JRRG VWXGHQWV KDG WRWDOOHG, EB FRQWUDVW, 8,000 KRXUV, DQG WKH IXWXUH PXVLF WHDFKHUV MXVW RYHU 4,000 KRXUV.
VR LW PDB EH WKDW 10,000 KRXUV, QRW 10 BHDUV, LV WKH PDJLF QXPEHU. (KHQUL FDUWLHU-EUHVVRQ (1908-2004) VDLG "BRXU ILUVW 10,000 SKRWRJUDSKV DUH BRXU ZRUVW," EXW KH VKRW PRUH WKDQ RQH DQ KRXU.) VDPXHO MRKQVRQ (1709-1784) WKRXJKW LW WRRN HYHQ ORQJHU: "HAFHOOHQFH LQ DQB GHSDUWPHQW FDQ EH DWWDLQHG RQOB EB WKH ODERU RI D OLIHWLPH; LW LV QRW WR EH SXUFKDVHG DW D OHVVHU SULFH." DQG FKDXFHU (1340-1400) FRPSODLQHG "WKH OBI VR VKRUW, WKH FUDIW VR ORQJ WR OHUQH." KLSSRFUDWHV (F. 400EF) LV NQRZQ IRU WKH HAFHUSW "DUV ORQJD, YLWD EUHYLV", ZKLFK LV SDUW RI WKH ORQJHU TXRWDWLRQ "DUV ORQJD, YLWD EUHYLV, RFFDVLR SUDHFHSV, HASHULPHQWXP SHULFXORVXP, LXGLFLXP GLIILFLOH", ZKLFK LQ HQJOLVK UHQGHUV DV "OLIH LV VKRUW, [WKH] FUDIW ORQJ, RSSRUWXQLWB IOHHWLQJ, HASHULPHQW WUHDFKHURXV, MXGJPHQW GLIILFXOW." DOWKRXJK LQ ODWLQ, DUV FDQ PHDQ HLWKHU DUW RU FUDIW, LQ WKH RULJLQDO JUHHN WKH ZRUG "WHFKQH" FDQ RQOB PHDQ "VNLOO", QRW "DUW". """
print deCaesar(txt)
3-24. What is the best data structure for maintaining URLs that have been visited by a Web crawler? Give an algorithm to test whether a given URL has already been visited, optimizing both space and time.
Solution: An easy way is to use a hash table for the domains and a hash table for paths.
function testURL
calculate hash function of domain
look up in hash table for domains
if multiple entries:
traverse until you find right domain
if path not found
return Not found
calculate hash function of path
look up in hash table for path
if multiple entries:
traverse until you find right domain
if path not found
return Not found
3-28. You have an unordered array X of n integers. Find the array M containing n elements where Mi is the product of all integers in X except for Xi. You may not use division. You can use extra memory. (Hint: There are solutions faster than )
Solution: Here’s a algorithm which works in :
First we use our extra memory to store multiplications. We multiply numbers together. This takes
Now we just need to find our number by using this pre-multiplications and one element of the original array. This takes for all M about
time. Therefore we have
total run time.
Example:
X = [6, 5, 3, 1, 7, 6, 2, 3] Y = [6*5*3, 5*3*1, 3*1*7, 1*7*6, 7*6*2, 6*2*3, 2*3*6, 3*6*5] M1 = [Y[2] * Y[5] * X[8]] M2 = [Y[3] * Y[6] * X[1]] M3 = [Y[4] * Y[7] * X[2]] M4 = [Y[5] * Y[8] * X[3]] M5 = [Y[6] * Y[1] * X[4]] M6 = [Y[7] * Y[2] * X[5]] M7 = [Y[8] * Y[3] * X[6]] M8 = [Y[1] * Y[4] * X[7]]