graph

6-3. Assume that all edges in the graph have distinct edge weights (i.e. , no pair of edges have the same weight). Is the path between a pair of vertices in a minimum spanning tree necessarily a shortest path between the two vertices in the full graph? Give a proof or a counterexample.

Solution Let’s start with an example.

Our minimum spanning tree is marked by the thick edges. We are interested in the path between B and D. We’re interested in the weight b. If b is smaller than 5, the MST (minimum spanning tree) isn’t the shortest path. Would this change our MST? It depends. We could form the graph from B -> D -> C instead of B -> C -> D. It would be our MST if $b + 3 < 2 + 3$ , i.e. $e \in [0, 2] \setminus \{1, 2\}.$ In conclusion, the MST isn’t the shortest path if $2 < b < 5.$

6-6. Suppose we are given the minimum spanning tree T of a given graph G (with n vertices and m edges) and a new edge e = (u, v) of weight w that we will add to G. Give an efficient algorithm to find the minimum spanning tree of the graph G + e. Your algorithm should run in O(n) time to receive full credit.

Solution

We are interested into each path going from u to v. In this example there is the initial path u->t->v and the new one u->v. Now we can check which one is shorter and take this one. The rest of the tree isn’t affected by this.

6-7. (a) Let T be a minimum spanning tree of a weighted graph G. Construct a new graph G′ by adding a weight of k to every edge of G. Do the edges of T form a minimum spanning tree of G′? Prove the statement or give a counterexample.

(b) Let P = {s, . . . , t} describe a shortest weighted path between vertices s and t of a weighted graph G. Construct a new graph G′ by adding a weight of k to every edge of G. Does P describe a shortest path from s to t in G′? Prove the statement or give a counterexample.

Solution (a) The order of the weights aren’t affected by the addition therefore it still forms the MST: $a + c < b + c = a < b$ .

(b) No, see the counter example in the comments by Matus Goljer. Thanks for that!

6-23. Arbitrage is the use of discrepancies in currency-exchange rates to make a profit. For example, there may be a small window of time during which 1 U.S. dollar buys 0.75 British pounds, 1 British pound buys 2 Australian dollars, and 1 Australian dollar buys 0.70 U.S. dollars. At such a time, a smart trader can trade one U.S. dollar and end up with 0.75 × 2 × 0.7 = 1.05 U.S. dollars—a profit of 5%. Suppose that there are n currencies c1 , …, cn and an n × n table R of exchange rates, such that one unit of currency ci buys R[i,j] units of currency cj. Devise and analyze an algorithm to determine the maximum value of

R[c1, ci1] · R[ci1, ci2] · · · R[cik−1, cik] · R[cik, c1]

Solution Here’s the example as a graph.

The first problem is that maximum path algorithms don’t multiply the values the add them. This problem can be solved by using logarithms: $\log(a \cdot b \cdot c) = \log(a) + \log(b) + \log(c).$

EDIT: Please see the entry in the comments. Thanks

5-6. In breadth-first and depth-first search, an undiscovered node is marked discovered when it is first encountered, and marked processed when it has been completely searched. At any given moment, several nodes might be simultaneously in the discovered state.
(a) Describe a graph on n vertices and a particular starting vertex v such that Θ(n) nodes are simultaneously in the discovered state during a breadth-first search starting from v.
(b) Describe a graph on n vertices and a particular starting vertex v such that Θ(n) nodes are simultaneously in the discovered state during a depth-first search starting from v.
(c) Describe a graph on n vertices and a particular starting vertex v such that at some point Θ(n) nodes remain undiscovered, while Θ(n) nodes have been processed during a depth-first search starting from v. (Note, there may also be discovered nodes.)

Solution. (a) A graph with n vertices and a depth of one where no node was processed yet which started at the root.
(b) A graph with n vertices and a depth of n where no node was processed yet which started at the root.
(c) E.g. the graph of (b) which is processed up to n/2.

5-7. Given pre-order and in-order traversals of a binary tree, is it possible to reconstruct the tree? If so, sketch an algorithm to do it. If not, give a counterexample. Repeat the problem if you are given the pre-order and post-order traversals.

Solution I made this example to simplify the process of reconstructing the binary tree.

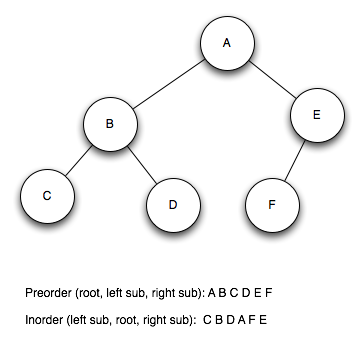
It’s essential to understand preorder and inorder traversal. Let’s take a look at the preorder sequence: A B C D E F
We know that A has to be our root. We don’t know yet if B is the right or left child. Therefore let’s look at the inorder sequence: C B D A F E
Oh, A is on the 4th position, i.e. C, B and D have to be in the left subtree. Therefore B is the left child. Now we have C and D left in the left subtree. Let’s look again at the inorder sequence: C B D A. So C has to be the far left node and because B is the left child D have to be the right child of B.
Now we have to find out where E and F belong. We know that they belong to a right subtree to A. If you look at the preorder sequence you see that E has to be the root of the left subtree. Finally we look at the inorder sequence and see that F is before E. Therefore F has to be the left sub because E is the root and we’re done.

5-8. Present correct and efficient algorithms to convert an undirected graph G be- tween the following graph data structures. You must give the time complexity of each algorithm, assuming n vertices and m edges.
(a) Convert from an adjacency matrix to adjacency lists.
(b) Convert from an adjacency list to an incidence matrix. An incidence matrix M has a row for each vertex and a column for each edge, such that M[i,j] = 1 if vertex i is part of edge j, otherwise M[i,j] = 0.
(c) Convert from an incidence matrix to adjacency lists.

Solution (a)

for y := 1 to n
    for x := y to n
        if matrix[x][y] = 1
            addEdge(x, y)

Which runs in 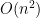$O(n^2)$ time.

(b)

initialize matrix[m][n]
x := 1
for each entry in list
    matrix[x][from] = 1
    matrix[x][to] = 1

We need 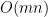$O(mn)$ for initializing the matrix and the loop needs 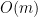$O(m)$ therefore the algorithm needs 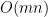$O(mn)$ time.

(c)

for x := 1 to n
    start := None
    end := None
    for y := 1 to n
        if matrix[x][y] = 1
            if start = None
                start := y
            else if end = None
                end := y
    addEdge(start, end)

This algorithm also takes $O(n^2)$ time.

5-9. Suppose an arithmetic expression is given as a tree. Each leaf is an integer and each internal node is one of the standard arithmetical operations (+,−,∗,/). For example, the expression 2 + 3 ∗ 4 + (3 ∗ 4)/5 is represented by the tree in Figure 5.17(a). Give an O(n) algorithm for evaluating such an expression, where there are n nodes in the tree.

Solution

function evaluateTree
    if tree->left-subtree and tree->right-subtree is not a expression
        return evaluate(tree, tree->left-subtree->value, tree->right-subtree->value)
    else 
        if tree->left-subtree is a expression
            left := evaluateTree(tree->left-subtree)
        else
            left := tree->left-subtree->value

        if tree->right-subtree is a expression
            right := evaluateTree(tree->right-subtree)
        else
            right := tree->right-subtree->value

        return evaluate(tree, left, right)

5-18. Consider a set of movies M1, M2, . . . , Mk. There is a set of customers, each one of which indicates the two movies they would like to see this weekend. Movies are shown on Saturday evening and Sunday evening. Multiple movies may be screened at the same time.
You must decide which movies should be televised on Saturday and which on Sun- day, so that every customer gets to see the two movies they desire. Is there a schedule where each movie is shown at most once? Design an efficient algorithm to find such a schedule if one exists.

Solution We can model this problem as a graph problem. Each node is a movie and each edge (x, y) represents a person who wants to watch movie x and y.

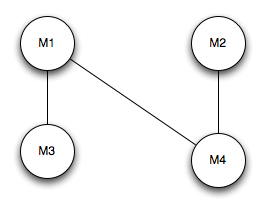
For example: People want to watch movie 1 & 3, 1 & 4 and 2 & 4. Here we can show movie 1 and 2 on saturday and movie 3 and 4 on sunday because there isn’t a connection between movie 1 and 2 and movie 3 and 4. That is, nobody wants to see movie 1 and 2 or movie 3 and 4.
Let’s add an edge between movie 1 and 2 and see what’s happen.

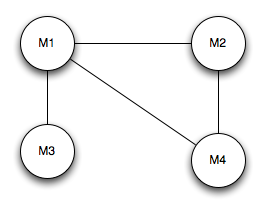
Our last schedule doesn’t work anymore because movie 1 and movie 2 are screened on the same day. We’re looking for a bipartite graph which is discussed early in the book.

5-23. Your job is to arrange n ill-behaved children in a straight line, facing front. You are given a list of m statements of the form “i hates j”. If i hates j, then you do not want put i somewhere behind j, because then i is capable of throwing something at j.
Give an algorithm that orders the line, (or says that it is not possible) in O(m + n) time.

Solution We can save us a lot of time if we model the problem correctly.

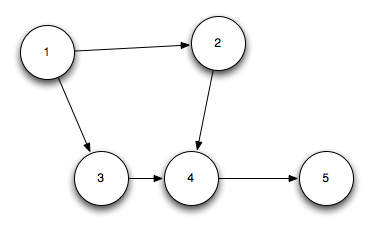
In this example 1 hates 2 and 3, 2 hates 4, 3 hates 4, and 4 hates 5. You can see that we can use topological sorting for this problem which is also described early in the book.

The Algorithm Design Manual: Chapter 6

The Algorithm Design Manual: Chapter 5